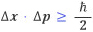|
양자물리학 이야기를 하면서 불확정성의 원리 이야기를 하지 않을 수 없다. 독일의 물리학자 베르너 하이젠베르크(Werner Heisenberg, 1901~1976)가 제안한 불확정성의 원리는 코펜하겐 해석의 핵심 내용 중의 하나이다. 많은 물리학 해설서나 현대 물리학 입문서에서 불확정성의 원리를 다루고 있어 불확정성 원리는 양자 물리학의 내용 중 가장 많은 사람에게 알려진 내용이기도 하다. 하지만 수학을 떠나서 불확정성 원리를 정확하게 설명하는 것은 쉬운 일이 아니다. 따라서 불확정성 원리에 대해 많은 것을 들어서 알고 있는 사람들도 조금씩 잘못 알고 있는 경우가 많다. 불확정성의 원리는 말 그대로 확실하지 않다는 원리이다. 확실한 것만을 다루는 것으로 알려진 물리학에 왜 이런 원리가 등장하게 되었을까? 무엇이 왜 불확실하다는 것일까?
수많은 사인과 코사인 파동의 합으로 입자를 표현하는 웨이브 패킷
 |
|

불확정성의 원리를 발표하여 코펜하겐 해석의 발전에 큰 기여를 한 하이젠베르크 하이젠베르크는 이 업적으로 1932년 노벨 물리학상을 받았다.
<출처: 노벨상 위원회> | |
|
|
전자와 같은 입자도 파동의 성질을 가지고 있다는 것은 실험을 통해 확인되었다. 양자 물리학은 불연속적인 물리량을 가지는 입자를 파동함수로 다루고, 그 결과를 확률로 해석하는 물리학이다. 입자를 파동방정식으로 다루기 위해서는 입자도 파동함수로 나타낼 수 있어야 할 것이다. 그렇다면 입자를 어떻게 파동함수로 나타낼 수 있을까?
고등학교에서 물리학을 배운 사람들은 사인(sine) 또는 코사인(cosine)과 같은 삼각함수로 파동을 표현하는 법에 대해서 들어본 적이 있을 것이다. 그러나 이런 파동으로 입자를 나타내기는 어렵다. 파동이 넓은 공간에 퍼져 있는 것과는 달리 입자는 아주 좁은 공간에 집중되어 있기 때문이다.
그러나 수학을 이용하면 이 문제를 쉽게 해결할 수 있다. | |
| 진동수와 진폭이 다른 많은 파동을 합치면 한 곳에 집중된 파동을 만들어 낼 수 있다. 만약 더 좁은 구역에 집중된 파동을 만들고 싶으면 파장이 다양한 더 많은 사인파와 코사인파를 더하면 된다. 이렇게 여러 개의 파동을 합성하여 만들어진 파동을 양자 물리학에서는 웨이브 패킷이라고 부른다. 양자 물리학에서 입자는 웨이브 패킷을 이용하여 나타내진다. | |


분산되지 않는 웨이브 패킷을 통해 입자를 표현할 수 있다.
<출처: Jmtrivial at en.wikipedia.com>

|
위치와 운동량을 곱하면 일정한 숫자보다 항상 크다 : 불확정성의 원리

입자는 이 웨이브 패킷 내의 어느 곳에 있게 된다. 따라서 웨이브 패킷의 너비가 좁으면 입자의 위치에 대한 불확실성이 작아지고 반대로 웨이브 패킷의 너비가 커지면 위치에 대한 불확실성이 커진다. 좁은 너비를 가지는 웨이브 패킷을 만들기 위해서는 다른 진동수를 가지는 더 많은 파동을 합해야 한다. 입자의 운동량은 진동수에 비례하고 따라서 파장에 반비례한다. 그러므로 좁은 너비를 가지는 웨이브 패킷을 만들기 위해 다른 진동수를 가지는 많은 파동을 합하게 되면 운동량의 불확실성은 커진다. 다시 말해 위치 측정의 오차를 줄이려고 하면 운동량 측정의 오차가 증가한다는 것이다. 이것이 위치와 운동량 사이에 존재하는 불확정성이다. 하이젠베르크는 위치의 오차와 운동량 오차의 곱은 일정한 값 이상일 수밖에 없다는 것을 수학적으로 증명했다. 이것을 식으로 나타내면 다음과 같다.
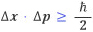
이 식에서 Δx는 위치의 오차를 나타내고 Δp는 운동량의 오차를 나타내며 ℏ는 플랑크 상수를 2π로 나눈 값이다. 불확정성의 원리 때문에 위치와 운동량을 동시에 정확하게 측정하는 것은 불가능하다. 이러한 불확정성의 원리는 시간과 에너지 사이에도 존재한다. 어떤 양들 사이에 불확정성이 존재하는지를 설명하는 것은 간단하지 않다. 다만 여기서는 위치와 운동량, 그리고 에너지(질량)와 시간 사이에 불확정성의 원리가 적용된다는 것을 알고 있는 것으로 충분하다고 생각한다.
불확정성의 원리, 하나를 측정하는 동안 다른 하나가 변화한다

불확정성의 원리는 위치의 측정이 운동량을 변화시키고, 반대로 운동량의 측정이 위치를 변화시켜 오차를 증가시키기 때문이라고 설명하기도 한다. 이런 설명은 잘못된 설명이 아니다. 하이젠베르크와 보어도 이런 방법으로 불확정성 원리를 설명하려고 시도했다. 물리학 입문서에 자주 등장하는 것도 이런 설명이다. 예를 들면 다음과 같은 설명이다. | |
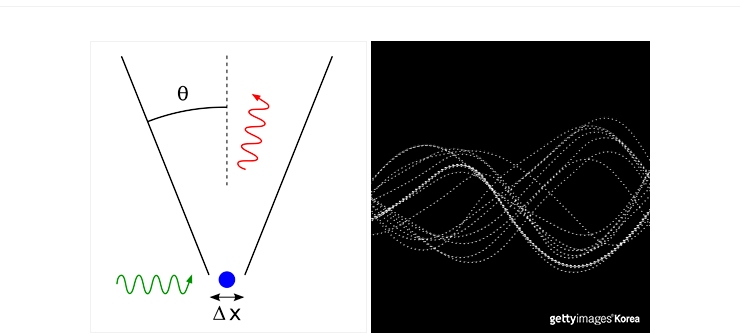
하이젠베르크가 제안한 감마선 현미경의 개념도(왼쪽) 입자를 파동의 중첩으로 표현하며 알게 된 불확정성의 원리는
측정때문에 생기는 것이 아니라 입자 자체가 가지고 있는 물리적인 성질에서 기인한다.(오른쪽)
<출처: parri ar en.wikipedia.com(왼쪽)>

|
전자를 관찰할 수 있는 현미경이 있다고 가정해 보자. 이 현미경으로 전자를 관측하기 위해서는 전자에 충돌한 빛이 현미경으로 들어와야 한다. 전자의 위치를 정확하게 측정하기 위해서는 파장이 짧아서 에너지가 큰 빛을 사용해야 한다. 이런 빛으로는 전자의 위치를 작은 오차로 측정할 수 있지만, 측정 과정에서 전자의 운동량을 크게 변화시킨다. 반대로 운동량의 변화를 최소로 하여 운동량의 오차를 줄이려고 하면, 빛의 긴 파장 때문에 위치에 오차가 커질 수밖에 없다. 따라서 위치와 운동량을 동시에 정확하게 측정하는 것이 불가능하다는 것이다.
그러나 이러한 설명은 불확정성의 원리를 입자의 기본 성질이 아니라 측정 과정 때문에 나타나는 효과라고 생각하게 하기 쉽다. 하이젠베르크와 보어는 이런 설명을 논리적인 인식론의 철학적 체계 안에서 사용했다. 논리적인 인식론에서는 어떤 계의 물리적 성질은 측정 가능한 가장 정확한 측정값에 의해 나타나는 것이라 본다. 이것을 다르게 표현하면 만약 어떤 측정값이 이론적으로 어떤 오차보다 더 작아질 수 없다면, 이러한 한계는 물리적 성질 때문이지 측정 장치나 측정 기술 때문이 아니라는 것이다. 다시 말해 불확정성 원리는 측정 때문에 생기는 것이 아니라, 측정하고자 하는 입자 자체가 가지고 있는 물리적 성질에 기인한다는 것이다.
아인슈타인, 사고실험을 통해 불확정성 원리에 대한 반론을 제기하였다
 | |
|
결정론을 받아들이고 있던 과학자들은 불확정성 원리를 받아들이지 않았다. 1927년에 코펜하겐 해석이 제안되었을 때, 아인슈타인과 슈뢰딩거를 비롯한 많은 과학자가 가장 격렬하게 비판한 내용 중의 하나가 바로 불확정성의 원리였다. 코펜하겐 해석에 의하면 양자물리학을 이용하여 어떤 실험결과를 얻을 수 있는지를 계산할 수는 있지만, 입자가 실제로 어떤 상태인지를 알 수는 없다. 다시 말해 파동 방정식이 말해 주는 것은 입자가 어떤 상태에 있는지가 아니라 실험을 했을 때 우리가 어떤 값을 얻을 것인지를 이야기해 줄 뿐이다.
아인슈타인은 측정 결과가 확률로 나타내지는 것은 우리가 실제 입자의 행동을 규제하는 변수들을 모두 알지 못하기 때문이라고 주장했다. 아인슈타인의 이런 주장을 숨은 변수이론이라고 부른다는 것은 이전 글에서 언급한 적이 있다. 이에 대해 보어는 확률적인 결과는 입자가 가지고 있는 기본적인 성질에 기인하는 것이어서 측정 장치와는 관계없으며 결코 줄일 수 없는 것이라고 주장했다.
불확정성 원리를 비판하기 위해 아인슈타인은 다음과 같은 사고실험을 제안했다. 사고실험은 원리의 진위를 따져보기 위한 가상적인 실험이므로 실제로 그런 실험이 가능하냐 하는 것과는 관계없다. | |
|
|

시간과 에너지 사이의 불확정성을 반박하기 위해,
아인슈타인은 빛이 나올 수 있는 박스를 이용한 사고실험을 제안하였다. | |
|
아인슈타인은 멀리서 날아온 입자가 벽에 난 작은 슬릿을 통과하는 경우를 예로 들었다. 만약 이 입자가 크기가 d인 슬릿을 통과한다고 가정하면 벽을 통과하는 동안 이 입자의 위치의 오차는 d보다 클 수 없다. 따라서 불확정성의 원리에 의하면 운동량의 오차는 약 ℏ/d이상이어야 한다.
그러나 만약 입자가 슬릿을 통과하는 동안에 벽의 운동량의 변화를 측정한다면 슬릿을 통과한 입자의 운동량을 얼마든지 정확하게 계산할 수 있다. 입자가 벽에서 멀리 떨어져 있을 때, 이 입자의 운동량을 원하는 만큼 정확하게 측정하여 알고 있고, 입자가 벽에 난 슬릿을 통과하는 동안 벽 운동량의 변화가 없었다면, 이 입자의 운동량은 운동량 보존 법칙에 의해 이전의 운동량과 같은 값을 가져야 한다. 그러나 만약 벽을 통과하는 동안 벽과의 상호작용으로 인해 벽의 운동량에 변화가 생겼다면 이 값으로부터 전자의 정확한 운동량을 알 수 있다는 것이다. 그렇게 되면 불확정성의 원리는 더는 성립하지 않는다.
아인슈타인의 이런 주장에 대해 보어는 입자뿐만 아니라 벽도 양자 역학의 지배를 받는다는 것을 지적했다. 따라서 벽의 운동량 변화를 측정하여 입자의 운동량 변화를 측정하려면, 입자가 벽을 통과하기 전후의 벽의 운동량을 정확하게 측정할 수 있어야 한다. 그러나 벽의 운동량을 정확하게 측정하려면 벽의 위치의 오차가 발생하게 되고 이는 입자의 위치 오차를 증가시키기 때문에 불확정성 원리는 이 사고실험에서도 성립한다는 것을 보여 주었다.
아인슈타인의 이론으로 아인슈타인의 반론을 잠재웠다

아인슈타인은 시간과 에너지 사이의 불확정성을 비판하기 위해 또 다른 사고실험을 제안했다. 이 사고실험에서는 빛 입자가 들어 있는 상자에 정밀한 시계 장치가 되어 있는 창문이 달렸다고 가정했다. 창문에 달린 시계 장치를 이용하여 정확한 시각에 창문이 열렸다 닫히고 이때 에너지가 밖으로 나간다고 가정해보자. 창문을 열었다 닫는 시간을 정확히 측정하고 창문 열고 닫기 전후의 상자 전체의 무게를 정확하게 측정하면 빛이 상자를 탈출하는 시간과 빛이 가지고 달아난 에너지의 양을 원하는 만큼 정확하게 측정할 수 있다는 것이다. 그렇게 되면 시간과 에너지의 양을 동시에 정확하게 측정할 수 없다는 불확정성 원리는 더는 성립하지 않게 된다.
보어는 이 사고실험도 불확정성의 원리 내에서 해결했다. 그는 상자가 가진 에너지의 양을 정확하게 알면 창문을 여닫는 시간이 부정확해질 수밖에 없다는 것을 증명했다. 상자와 상자의 질량을 측정하는 저울은 모두 중력장 안에 있다. 중력장 안에서의 시계의 위치에도 오차가 있을 수밖에 없고 위치에 따라 중력의 크기가 다르므로 위치의 오차는 일방상대성이론에 의해 시간의 오차를 불러온다는 것이다. 중력이 시간의 흐름에 영향을 준다는 것을 밝혀낸 사람은 아인슈타인이었다. 그러나 아인슈타인은 쉽게 포기하지 않았다. 1935년에 그는 로젠, 포돌스키와 함께 불확정성 원리와 코펜하겐 해석을 비판하는 EPR 패러독스를 발표했다. 다음 이야기에서는 아인슈타인이 제시한 EPR 패러독스에 대한 내용을 알아보자.
| |